Équations algébriques

Avant de commencer cette section, assurez-vous de connaître avec les règles qui déterminent l'ordre des opérations dans les équations mathématiques. Il est nécessaire de savoir dans quel ordre additionner, soustraire, diviser et multiplier pour résoudre une équation.

Dans les équations algébriques, on utilise des lettres et des symboles pour représenter les nombres inconnus. Pour résoudre ces problèmes, il faut isoler la variable inconnue. Commençons avec quelques exemples simples.

Pour résoudre une équation algébrique, il faut connaître de connaître les opérations mathématiques opposées. Par exemple, la soustraction est l'opposé de l'addition et la division est l'opposé de la multiplication. Extraire la racine carrée d'un nombre est l'opposé de l'élever au carré. (Nous n'étudierons pas les racines carrées dans la présente section.)

Exemple 1

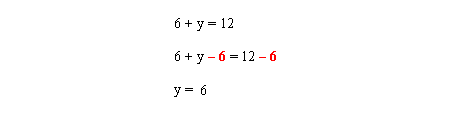
Pour isoler Y, il faut éliminer le +6 du côté gauche de l'équation. Dans toute équation algébrique, peu importe ce qu'on fait d'un côté de l'équation, on doit le faire également de l'autre côté. Dans ce cas-ci, on soustrait 6 des deux côtés.

Exemple 2

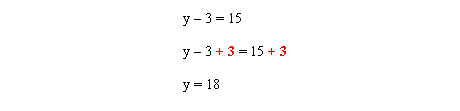
Pour isoler Y, il faut éliminer le -3 du côté gauche de l'équation. On additionne donc 3 des deux côtés.

Exemple 3

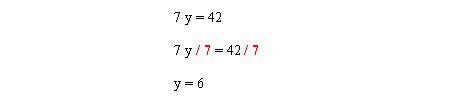
Dans ce cas-ci, Y est multiplié par 7. Pour éliminer le nombre qui multiplie, il faut diviser par le même nombre. On divise donc les deux côtés de l'équation par 7.

Exemple 4

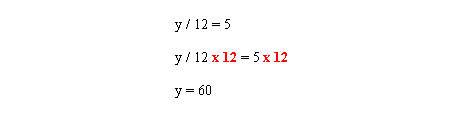
Dans ce cas, Y est divisé par 12. Pour éliminer le nombre qui divise, il faut multiplier par le même nombre. On multiplie donc les deux côtés de l'équation par 12.

Équations à résoudre

Exercez-vous à résoudre ces équations simples. Les réponses sont données à la fin de la page.

1) y / 11 = 23
2) 15 + y = 63
3) – 5 + y = 10
4) 13 (y) = 130
5) 5 y = 15
6) 6 + 3 + y = 56
7) 2(y) = 56
8) y / 8 = 4
9) y (24) = 72

Équations algébriques avancées

Lorsque vous avez à résoudre des équations, vous devez respecter les règles de l'ordre des opérations, qui prescrivent de faire d'abord les opérations entre les parenthèses, suivies des exposants, ensuite les divisions et les multiplications et, en dernier lieu, les additions et les soustractions. Lorsque vous isolez des variables inconnues, suivez l'ordre inverse. (Nous ne couvrirons pas les équations avec exposants à cette étape-ci.)

Exemple 5

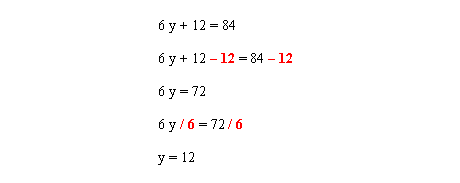
Pour isoler Y, il faut d'abord éliminer le +12 du côté gauche de l'équation. Pour cela, on soustrait 12 des deux côtés. L'équation est maintenant : 6y = 72. Pour isoler Y, il suffit de diviser les deux côtés de l'équation par 6.

Exemple 6

Vous pouvez avoir à résoudre des équations dont l'un des côtés exige des opérations sans variable inconnue. Dans de tels cas, il faut d'abord résoudre le côté sans variable inconnue EN RESPECTANT LES RÈGLES ÉTABLIES DE L'ORDRE DES OPÉRATIONS.

Après cela, il s'agit de résoudre l'équation dans la manière habituelle. Les personnes plus avancées en mathématiques seront capables de regrouper des éléments du côté gauche également, mais à moins de se sentir vraiment à l'aise, il vaut mieux de procéder du côté gauche de la façon indiquée.

Exemple 7

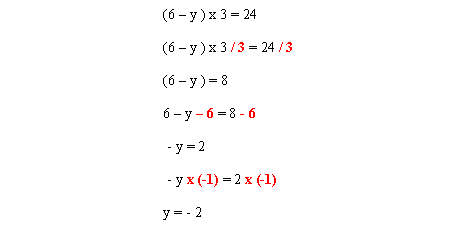
Il faut résoudre l'équation en suivant les règles établies. Laissez les opérations entre parenthèses jusqu'à la fin. Lorsqu'il restera que des opérations entre parenthèses, vous pourrez supprimer celles-ci, car elles seront alors inutiles.

Lorsque l'équation a été réduite au point où l'inconnue est complètement isolée mais négative, multipliez simplement les deux côtés de l'équation par -1 pour inverser les signes.

La réponse du problème ci-dessus est : y = -2.

Exemple 8

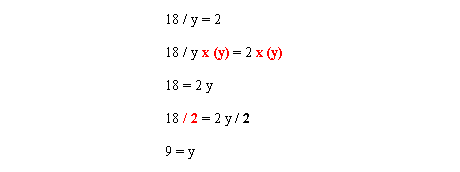
Un autre problème délicat que vous pourriez rencontrer est celui où Y figure comme dénominateur dans une équation de division. Pour transformer Y en numérateur, il faut multiplier les deux côtés de l'équation par Y. L'équation est maintenant : 18 = 2y. Il reste à résoudre l'équation de la façon habituelle

PEU IMPORTE CE QUE VOUS FAITES D'UN CÔTÉ DE L'ÉQUATION, VOUS DEVEZ LE FAIRE ÉGALEMENT DE L'AUTRE CÔTÉ.

Autres équations à résoudre

a) 3 (y) + 6 – 10 = 89
b) (y) / 6 + 24 – 2 = 14
c) - y (3) +55 = 105
d) 5 y – 32 = 24 (3)
e) –32 + 6y/2 = 64
f) 22 y + 16 (8) = 6 y

Réponses

1) 253
2) 48
3) 15
4) 10
5) 3
6) 47
7) 28
8) 32
9) 3

a) 31
b) - 48
c) –16.7
d) 20.8
e) 32
f) – 8